FORMULARIOS, TABLAS Y CONSTANTES DE MATEMÁTICAS
TRIGONOMETRÍA |
DEFINICIONES TRIGONOMÉTRICAS | ||
GRADOS | ÁNGULOS | RADIÁN |
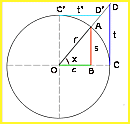
| Existen dos sistemas: Sexagesimal ==>> DEG (modo calculadora) Un círculo = 360º 1º = 60' y 1' =60'' Centesimal ==>> GRA (modo calculadora) Un círculo = 400 g 1g =100 m y 1m = 100 s | El radián es una unidad de ángulo. Se define como el ángulo cuyo arco tiene el mismo valor que el radio. x = 1 rad => OC=AC Un círculo tiene 2π rad (6,28 aprox.) π rad = 180º = 200 g (equivalencia) | |
s BA sen x = — = —— r OA | c OB cos x = — = —— r OA | t CD sen x tg x = — = —— = ———— r OC cos x |
1 OD' r cosec x = —— = —— = — sen x r s | 1 OD r sec x = —— = —— = — cos x r c | 1 C'D' cos x cotg x = — = —— = ——— tg x r sen x |
Si r = 1 | ||
| sen x = s | cos x = c | tg x = t |
| cosec x = OD' = s' | sec x = OD = c' | cotg x = C'D' = t' |
FÓRMULAS FUNDAMENTALES | ||
sen2 x + cos2 x = 1 | sec2 x - tg2 x = 1 | cosec2 x - cotg2 x = 1 |
VALORES QUE PUEDEN TOMAR LAS RAZONES TRIGONOMÉTRICAS | ||
-1≤ sen x ≤ 1 | -1≤ cos x ≤ 1 | -∞ ≤ tg x ≤ ∞ |
{cosec x ≤ -1} U {cosec x ≥ -1} | {sec x ≤ -1} U {sec x ≥ -1} | -∞ ≤ cotg x ≤ ∞ |
DEFINICIONES DE ÁNGULOS | ||
| Radián (rad) | Ángulo cuyo arco es igual al radio | |
| Grados sexagesimales (deg) | Ángulo recto = 90º ; 1º = 60' ; 1' = 60'' | |
| Grados centesimales (gra) | Ángulo recto = 100 g ; 1g = 100 m ; 1m = 100 s | |
| VALORES DE LAS RAZONES TRIGONOMÉTRICAS | ||||||||||||||||
| grad | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 |
| rad | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 |
| sen | — √0 —— 2 | — √ 1 —— 2 | — √ 2 —— 2 | — √ 3 —— 2 | — √ 4 —— 2 | — √3 —— 2 | — √2 —— 2 |
1 —— 2 | 0 | - 1 —— 2 | — -√ 2 —— 2 | — -√ 3 —— 2 | -1 | — -√ 3 —— 2 | — -√ 2 —— 2 | - 1 —— 2 |
| cos | — √ 4 —— 2 | — √ 3 —— 2 | — √ 2 —— 2 | — √ 1 —— 2 | — √ 0 —— 2 | - 1 —— 2 | — -√ 2 —— 2 | — -√3 —— 2 | -1 | — -√ 3 —— 2 | — -√ 2 —— 2 | - 1 —— 2 | 0 | 1 —— 2 | — √ 2 —— 2 | — √ 3 —— 2 |
| tg | 0 | — √ 3 —— 3 | 1 | — √ 3 |
--- | — -√3
| -1 | — -√3 —— 3 | 0 | — √ 3 —— 3 | 1 | — √ 3
| --- | — -√ 3
| -1 | — -√ 3 —— 3 |
| REGLA MNEMOTÉCTICA | ||||||||||||||||
RELACIONES TRIGONOMÉTRICAS | ||||||
| VALOR DE | EN FUNCIÓN DE: | |||||
| sen x | cos x | tg x | cotg x | sec x | cosec x | |
| sen x | 1 | ————— ±√ 1 - cos2 x | tg x —————— ————— ±√ 1 + tg2 x | 1 —————— ————— ±√ 1 - cotg2x | ————— ±√sec2 x - 1 ——————— sec x | 1 ————— cosec x |
| cos x | ————— ±√ 1 - sen2 x | 1 | 1 —————— ———— ±√1 + tg2 x | cotg x ——————— ————— ±√1 + cotg2x | 1 ————— sec x | —————— ±√cosec2 x - 1 ———————— cosec x |
| tg x | sen x ——————— ————— ±√ 1 - sen2 x | ————— ±√1 - cos2 x —————— cos x | 1 | 1 ————— cotg x | ————— ±√ sec2 x - 1 | 1 ——————— —————— ±√cosec2 x - 1 |
| cotg x | ————— ±√1 - sen2 x ——————— sen x | cos x ——————— ————— ±√1 - cos2 x | 1 ———— tg x | 1 | 1 ————— ———— ±√sec2 x -1 | —————— ±√ cosec2 x - 1 |
| sec x | 1 ——————— ————— ±√ 1 - sen2 x | 1 ————— cos x | ————— ±√1 + tg2 x | —————— ±√ 1 + cotg2x ———————— cotg x | 1 | cosec x ——————— —————— ±√ cosec2 x - 1 |
| cosec x | 1 ————— sen x | 1 ——————— ————— ±√ 1 - cos2 x | ————— ±√1 + tg2 x ——————— tg x | —————— ±√ 1 + cotg2x | sec x —————— ————— ±√ sec2 x -1 | 1 |
No hay comentarios:
Publicar un comentario